表面波探測中CMP分析
林宏一
（應用地質股份公司 OYO Corporation）
1.序言
土木建設領域的地質勘測中掌握10m的S波速度模型，在結構體耐震設計方面是非常重要的。以前，為了達到該目的，可以采用傳統孔中PS測井。另一方面，表面波（以下稱瑞利波）的位相速度主要反映地盤的S波速模型，所以能測量人工振動產生的表面波的位相速度，推斷地盤的S波速度的手法（表面波探測）也能嘗試應用。到目前為止，我國進行的表面波探測是通過計算兩個地震儀間的互相關，求出位相速度的方法，主要是采用振動器等激發定波動。
針對這種情況，Park et al.（1999）研究出了一種方法，將由重錘落下等沖擊震源而激發的震波，通過設置在測量線上的多個地震儀進行采集后，根據頻率領域的相對速度進行積分處理，將在時間-距離領域觀測到的波形，直接轉換成頻率-位相速度領域（的數據）（MASW：Multi-channel Analysis of Surface Waves）。該方法是由Park et al.（1999）提出，在兩個地震儀數據的互相關中，不僅能直觀分離困難的實體波和高次模式的表面波，而且具有能夠防止空間圖像失真問題的優點。Xia et al.（1999）多次采用該方法，做成了二次元S波速度斷面。
利用這種方法，為了能在低頻領域確定位相速度，如Park et al.(1999)中所指出的，需要將地震儀分布的長度范圍增加。但是，隨著分布長度的增長，在相同分布范圍內的速度模型即使發生變化，（地震儀的測試數據）也會將其平均化，從而可能降低空間方向的分辨率（林.鈴木，2000）。為提高空間分辨率，就需要在盡可能短的空間內確定位相速度，那么這個要求又與為測定速度需要收集盡可能長的范圍內的數據這一要求相矛盾。在這里，作者提出了解決這兩者矛盾的方法。
2.CMP分析
圖-1（a）是表面波探測記錄例。分布范圍的中央部分，表面波的后續波相對速度發生著明顯變化，我們認為這附近速度模型會變化。圖-1（b）是該數據頻率領域的相對速度。位相速度曲線分離成2根或3根，這樣采集位相速度就困難了。分析區間內速度模型變化時的離線曲線特征與林.西澤（2000）的物理模式實驗結果相協調。其中，為了簡化討論，Parketal（1999）的多波道分析認為，是從進行分析的全部跟蹤中，把正在研究的所有雙跟蹤組合抽出，計算的互相關之和。針對該想法，如果繪制互相關中心位置，使用的地震檢波儀的位置和中心位置的關系如圖-2（a）所示。互相關的中心位置存在于不同場所，所以分析區間內速度模型變化時，圖-1的位相速度精度就變低。為了防止這種情況，我們認為如圖-2（b），中心位置使用相同數據組合進行數據分析會比較有效果。以下，把這種分析稱作CMP（Common Mid Point）分析。但是，從一個起振點記錄中,假設僅采用形成的CMP組合進行分析，大量的組合就浪費了，以圖-2（a）為例，來自5個跟蹤正在研究的組合數是10組，CMP組合就成為兩組（圖-2（c））。Park et al.（1999）的多通道分析精度的好處是同時分析多個跟蹤，只采用CMP組合精度就變低。那么，研究的是振點不同的數據中，分析中心位置相同的數據，并計算離散曲線（圖-2（d））。下面總結了數據采集法和分析法。
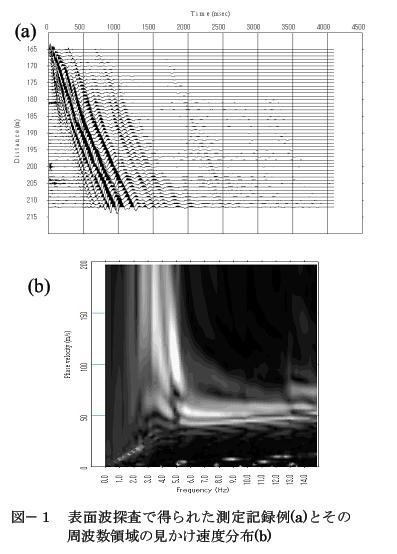
圖-1 表面波探測獲取的測量記錄例（a）
和其頻率領域的相對速度分布（b）
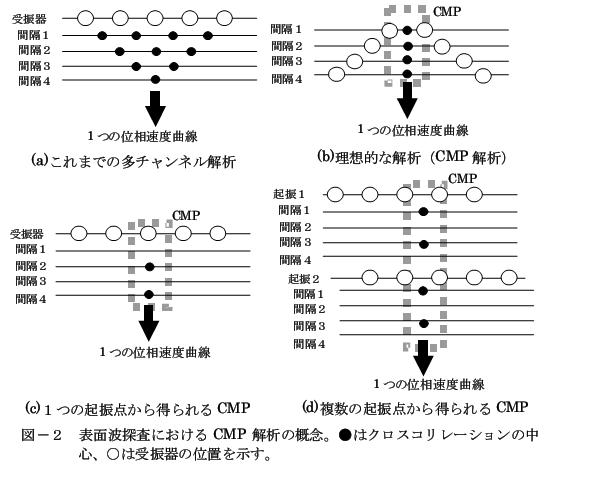
圖-2 表面波探測中CMP分析概念。●是互相關的中心，○是震檢波器的位置
3.數據采集法
數據采集類似于反射法地震探測。終端起振作為基礎，地震檢波器固定在測線端比較好（圖-3）。起振點間隔與受振點間隔相同是期望值，不過如果考慮到探測效率和分辨率，起振點間隔比受振點間隔粗點比較好。測量中，受振點間隔是0.5-2m，起振點間隔是2-4m。在反射法中，如果這種測量方法采用CDP電纜和CDP開關，就能很容易操作。
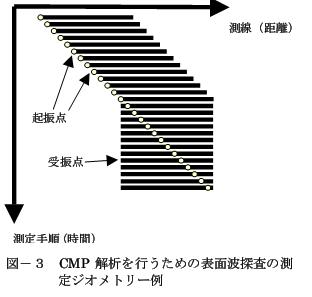
圖-3 CMP表面波探測的測量的幾何學例
4.分析法
對于采集的多個記錄，以前每次共同起振點記錄時都運用Park et al.（1999）的多通道分析，求出離散曲線。由此研究的CMP分析順序總結如下。
①首先，在獲取的所有共同起振點的每個記錄中，計算所有雙跟蹤組合的互相關。
②其次，從全起振點記錄中，收集相同場所雙跟蹤中間點的所有互相關。
③把相同受振點間隔的波重合，無論是相同受振點間隔，還是受振點間隔不同但有互相關，波形都可以重合在一起。
④中間點相等，不過受振點間隔不同的互相關無法直接重合。因此，首先重合求出的同一受振點間隔數據的互相關，再按照受振點間隔排列求出的記錄。這可以在位相速度分析中作為共同起振點間隔處理，根據受振點間隔抽出該地點的固有位相差。下面是模擬共同起振點記錄。
⑤模擬共同起振點記錄運用Park et al.（1999）的多通道分析。首先，每次跟蹤轉換成頻率領域，其次，按照起振點距離（受振點間隔）分配位相漂移，并使空間方向一體化。這樣就能將距離-時間的模擬共同起振點記錄轉換成頻率領域的相對速度分布。
⑥在頻率-位相速度圖表中，讀取每個頻率中振幅最大的位相速度，繪制位相速度曲線。
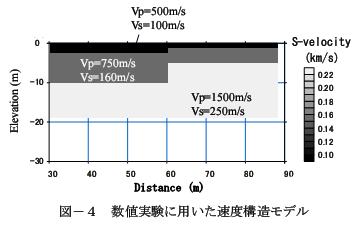
圖-4 數值實驗中采用的速度結構模式
5.數值實驗例
測量順序（時間）
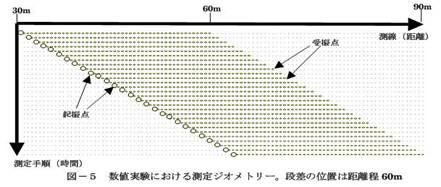
圖-5 數值實驗中測量幾何學。段差位置是60m距離左右。
為了顯示該方法的有效性，我們來進行一個數值實驗。圖-4是數值實驗中采用的模式，圖-5是測量的幾何學。圖-6是起振點位置35.8m的相同起振點記錄和其頻率領域的相對速度分布。段差位置是60m波形，相對速度就發生變化，位相速度曲線也分離成兩根。
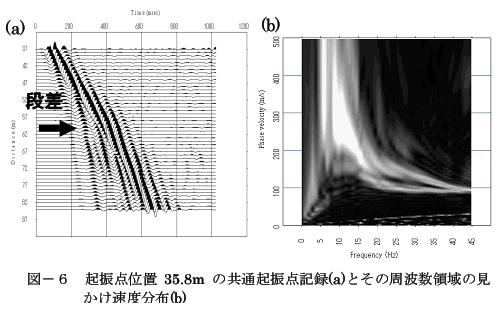圖-6 起振點位置35.8m的相同起振點記錄(a)和其頻率領域的相對速度分布(b)
針對該數據采用所有起振點記錄進行了CMP分析。圖-7顯示其結果。得知，在把形成CMP互相關按照受振點間隔排列的疑似共同起振點的記錄中，不存在共同起振點記錄中所見到的相對速度急劇變化。另外，用該頻率范圍相對速度的分布，得知位相速度匯總成1支。
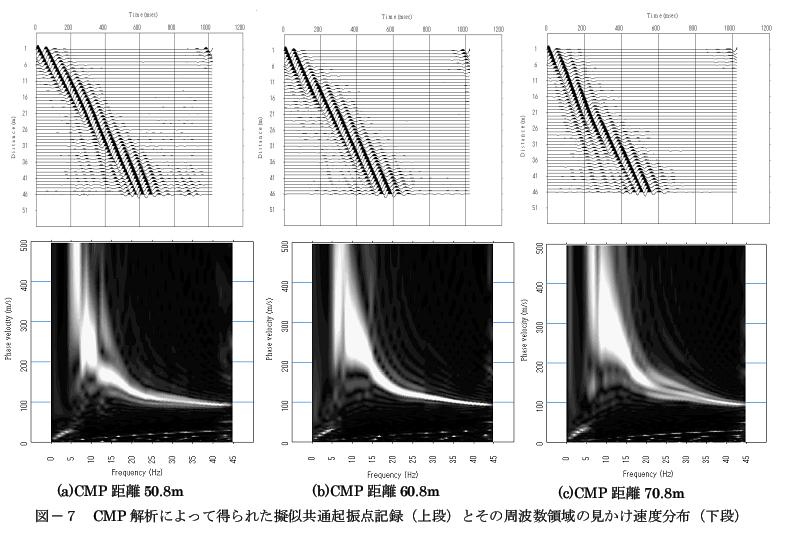
圖-7 CMP分析獲取的模擬相同起振點記錄（上段）和其頻率領域的相對速度分布（下段）
6.實際資料應用例
在圖-1中實際表面波探測記錄中應用該方法。圖-8顯示的是通過CMP分析獲取的疑似共同起振點記錄和其頻率領域的相對速度分布。在圖-1中，CMP距離分布的前半位置是173m及后半位置是201m。不存在共同起振點記錄中所見到的相對速度急劇變化，繼而得知離散曲線匯總成1支。
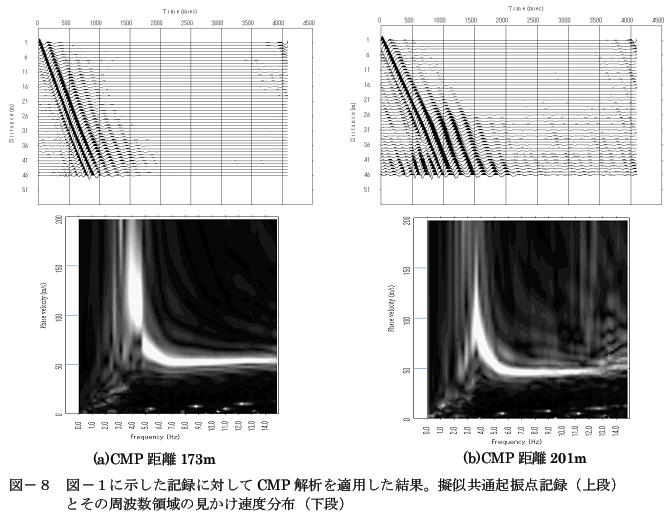
圖-8 對于圖-1中顯示的記錄應用CMP分析的結果。模擬相同起振點記錄（上段）和其頻率領域的相對速度分布（下段）
7.小結
采用人工振源的表面波探測中，簡單捕捉地基模型水平方向變化進行測量和分析。該方法的特點是：作為互相關處理多個起振點和受振點的波形數據，最后就沒必要進行位相或位相速度的加法和平均。以前采用兩個受振器的表面波探測，從間隔不同的受振器記錄中求出各自單獨的位相速度。如果受振器間隔比波長大，就無法通過空間圖像失真正確計算為位相速度。因此，只能分析采集波形記錄的一部分信息。針對這種情況，McMechan and Yedlin（1981）和Park et al.（1999）的多通道分析是一種從不同受振點間隔的多個波形記錄中求出直接位相速度的方法，能采用波形的所有信息。本論文發展了該方法，它是通過總結受振點間隔的不同記錄的互相關作為疑似共同起振點記錄，從不同起振點的多個記錄中就能直接計算出直接位相速度。通過采用該方法，不僅能在表面波探測的多通道分析中提高水平方向的分辨率，而且使用兩個受振器，即使以前的表面波探測的多通道分析也可以進行。
<參考文獻>
林 宏一.西澤 修，2001，采用激光多普勒效應示振器的表面波物理模型實驗，物理探測學會第104次學術演講會論文集，16-20.
林 宏一.鈴木晴彥，2000，二次元結構中表面波的傳播及其離散曲線，物理探測學會第103次學術演講會文集，226-230
技術支持：service@epc.com.hk
